In diesem ersten Tutorial werden wir uns wieder in die Programmierung mit Processing einarbeiten. Dazu werden wir drei Beispiele betrachten, welche uns Schritt für Schritt an die Programmierung mit Hilfe von Vektoren und Klassen heranführen. Die Beispiele sind auf dem Server zu finden.
P01_1_BouncingBall_ohne_Vektoren
| Code Block | ||||||
|---|---|---|---|---|---|---|
| ||||||
//Spatial Interaction
//ZHdK, Interaction Design
//iad.zhdk.ch
//Beispiel 01: Bouncing Ball ohne Vektoren
float x = 100;
float y = 100;
float xspeed = 2;
float yspeed = 2;
float size = 50;
void setup()
{
size(650, 200);
smooth();
}
void draw()
{
background(255);
//1.Speed und Position addieren = neue Position
x = x + xspeed;
y = y + yspeed;
//2.Kanten erkennen
if ((x > width-size/2) || (x < 0+size/2))
{
xspeed = xspeed * -1; //Umkehren
}
if ((y > height-size/2) || (y < 0+size/2))
{
yspeed = yspeed * -1; //Umkehren
}
//3.Ball darstellen
stroke(0);
strokeWeight(2);
fill(127);
ellipse(x, y, size, size);
} |
"Bouncing Ball" ohne Vektoren
Um den Einstieg in Processing zu schaffen schauen wir uns zunächst ein einfaches kleines Beispiel an (P01_1_BouncingBall_ohne_Vektoren). In diesem Beispiel sehen wir die uns vertraute Umgebung, sowie die grundlegende Programmstruktur von Processing mit:
| Code Block |
|---|
void setup() // |
...
wird einmal aufgerufen |
...
void draw() // |
...
wird permanent ausgeführt |
Wenn wir das Beispiel laufen lassen, sehen wir einen Ball, welcher sich innerhalb der mit size(width, heigthheight) festgelegten Grenzen bewegt. In der draw()-Routine Routine sind dafür drei wesentliche Schritte nötig:
1
...
) Position neu berechnen
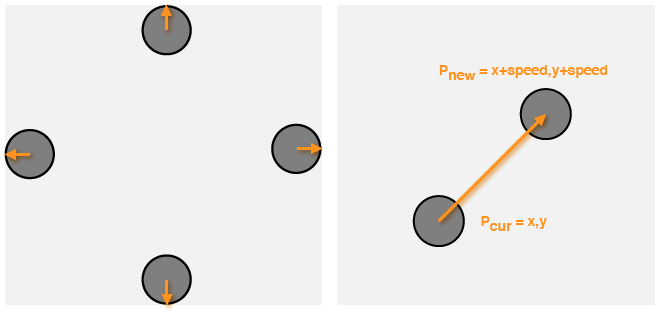
Die Position wurde zu Beginn mit den Variablen float x=100 und float y=100 festgelegt. Bei jedem Aufruf von draw() wird diese Position neu bestimmt, indem zur Ausgangsposition eine Geschwindigkeit hinzu addiert wird. Die Koordinaten der neuen Position lassen sich also mit x+=x+xspeed bzw. y+=y+yspeed berechnen.
2
...
) Auf Kollision mit den Kanten prüfen
Die Kollision mit den Kanten muss für jede der vier Kanten separat durchgeführt werden. Dazu benötigen wir sowohl die Position des Balls (x,y) und natürlich dessen Radius. Den Radius können wir berechnen indem wir die ursprünglich festgelegte Grösse float size = 50 durch 2 teilen. Also ergibt sich size/2. Diesen Radius testen wir dann zusammen mit der aktuellen Position auf Kollision mit den Rändern und kehren die Geschwindigkeit um z.B. xspeed *-1. Somit bewegt sich der Ball in der nächsten Itteration in die entgegengesetzte Richtung.
Links: x<0x < 0 + size / 2
Rechts: x>widthx > width - size / 2
Oben: y<0y < 0 + size / 2
Unten: y>heighty > height - size / 2
3
...
) Ball darstellen
Zuletzt legen wir fest, wie unser Ball dargestellt werden soll. Dazu geben wir ihm eine Farbe für die Umrandung stroke(0), legen fest, wie dick diese sein soll strokeWeight(2) und legen eine Füllfarbe fest fill(127). Danach zeichnen wir eine Ellipse an der Position, welche wir vorher berechnet haben ellipse(x,y,size,size).
...
| title | Merke |
|---|
...
Wichtig
- Position ist eine x und y Koordinate auf dem Screen
...
- Geschwindigkeit ist die Veränderung einer Position (Richtung und Betrag)
P01_1_BouncingBall_mit_Vektoren
| Code Block | ||||||
|---|---|---|---|---|---|---|
| ||||||
//Spatial Interaction
//ZHdK, Interaction Design
//iad.zhdk.ch
//Beispiel 02: Bouncing Ball mit Vektoren
PVector location;
PVector velocity;
float size = 50;
void setup()
{
size(650, 200);
smooth();
//Variablen initialisieren
location = new PVector(100,100);
velocity = new PVector(2,2);
}
void draw()
{
background(255);
//1.Speed und Position addieren = neue Position
location.add(velocity);
//2.Kanten erkennen
if ((location.x > width-size/2) || (location.x < 0+size/2))
{
velocity.x = velocity.x * -1; //Umkehren
}
if ((location.y > height-size/2) || (location.y < 0+size/2))
{
velocity.y = velocity.y * -1; //Umkehren
}
//3.Ball darstellen
stroke(0);
strokeWeight(2);
fill(127);
ellipse(location.x, location.y, size, size);
} |
...
"BouncingBall" mit Vektoren
Das obige Beispiel lässt sich mit Hilfe von Vektoren vereinfachen. Vektoren erlauben uns die Position und die Geschwindigkeit anders zu schreiben:
| Code Block | ||
|---|---|---|
| ||
float x; |
...
float y; |
...
float xspeed; |
...
float yspeed; |
wird zu:
Pvector
| Code Block | ||
|---|---|---|
| ||
PVector location; |
...
PVector velocity; |
Vektoren erlauben es uns also zwei Werte in einer Variablen zu speichern – bewegen wir uns im 3D Raum können auch drei Werte gespeichert werden. Vektoren sind also die Bezeichnung für eine Differenz zwischen sei Punkten in einem Raum.
Ein Vektor gibt uns also an, wie wir von einem Punkt zum nächsten gelangen. Zum Beispiel: Gehe in x-Richtung 10 Schritte und in y-Richtung -10 Schritte…
Wenn wir dies nun auf unser Beispiel anwenden, dann müssen wir folgende Änderungen vornehmen:
1
...
) Variablen initialisieren
Dazu deklarieren wir die Variablen PVector location und PVector velocity. Im setup()initialisieren wir dann die zuvor festgelegten Variablen und weisen ihnen Startwerte zu:
| Code Block | ||
|---|---|---|
| ||
location = new PVector(100,100); |
...
velocity = new PVector(2,2); |
2
...
) Position berechnen
Wie im ersten Beispiel müssen wir auch jetzt die neue Position anhand der letzten Position location und der Geschwindigkeit velocity berechnen. Dazu hilft es zu wissen, dass sich Vektoren sehr einfach miteinander addieren und subtrahieren lassen. Dies geschieht immer Komponentenweise, also separat für x-Werte und y-Werte
Um den Vektor w zu berechnen, welcher durch Addition von u und v zu erhalten ist, gilt folgendes Vorgehen:w = u + v
Auflösung nach Komponenten:wx = ux + vx
wy = uy + vy
In unserem Beispiel also:wx = 10 + 4 = 14
wy = -10 + 6 = -4
Um Objekte der Klasse PVector zu addieren verwenden wir in Processing den Begriff .add(). Wenden wir also dieses Wissen auf unser BouncingBall Beispiel an, so ändert sich:x = x + xspeed;
y = y + yspeed;
Zu:location.add(velocity);
3
...
) Auf Kollision mit den Kanten prüfen
Dieser Schritt ist nach wie vor nötig und wird lediglich in der Schreibweise für Vektoren angepasst. Dabei gilt zu beachten, dass die einzelnen Komponenten eines Vektors, also die x und x Werte mit einer Punktnotation erhalten werden können. Den x-Wert unserer Position erhält man folglich durch location.x und den y-Wert durch location.y.
4
...
) Ball darstellen
Die Darstellung bleibt auch gleich, bis auf die Schreibweise. Leider ist es nicht möglich ellipse(x,y,size,size) mit ellipse(location,size,size) zu ersetzen. Stattdessen schreiben wir wieder komponentenweise ellipse(location.x,location.y,size,size).
...
| title | Merke |
|---|
...
Wichtig
- Ein Vektor beschreibt die Differenz zwischen zwei Punkten
...
- Vektoren können zweidimensional (x,y) oder dreidimensional (x,y,z) sein.
...
- Vektoren lassen sich untereinander verrechnen (addieren, subtrahieren, dividieren, usw.)
Aufgaben
...
...
- Schaut euch die Beispiele 3 bis 6 an und versteht das Vorgehen.
...
...
//Spatial Interaction
//ZHdK, Interaction Design
//iad.zhdk.ch
//Beispiel 03: Vektoren subtrahieren
void setup()
{
size(650, 200);
smooth();
}
void draw()
{
background(255);
PVector mouse = new PVector(mouseX,mouseY);
PVector center = new PVector(width/2,height/2);
mouse.sub(center);
translate(width/2,height/2);
strokeWeight(2);
stroke(0);
line(0,0,mouse.x,mouse.y);
}| Code Block | ||||||
|---|---|---|---|---|---|---|
| ||||||
//Spatial Interaction
//ZHdK, Interaction Design
//iad.zhdk.ch
//Beispiel 04: Vektoren multiplizieren
void setup()
{
size(650, 200);
smooth();
}
void draw()
{
background(255);
PVector mouse = new PVector(mouseX,mouseY);
PVector center = new PVector(width/2,height/2);
mouse.sub(center);
mouse.mult(0.5);
translate(width/2,height/2);
strokeWeight(2);
stroke(0);
line(0,0,mouse.x,mouse.y);
} |
| Code Block | ||||||
|---|---|---|---|---|---|---|
| ||||||
//Spatial Interaction
//ZHdK, Interaction Design
//iad.zhdk.ch
//Beispiel 05: Vektoren vermassen
void setup()
{
size(650, 200);
smooth();
}
void draw()
{
background(255);
PVector mouse = new PVector(mouseX,mouseY);
PVector center = new PVector(width/2,height/2);
mouse.sub(center);
float m = mouse.mag();
fill(0);
noStroke();
rect(0,0,m,10);
translate(width/2,height/2);
stroke(0);
strokeWeight(2);
line(0,0,mouse.x,mouse.y);
} |
| Code Block | ||||||
|---|---|---|---|---|---|---|
| ||||||
//Spatial Interaction
//ZHdK, Interaction Design
//iad.zhdk.ch
//Beispiel 06: Vektoren normalisieren
void setup()
{
size(650, 200);
smooth();
}
void draw()
{
background(255);
PVector mouse = new PVector(mouseX,mouseY);
PVector center = new PVector(width/2,height/2);
mouse.sub(center);
mouse.normalize();
mouse.mult(150);
translate(width/2,height/2);
stroke(0);
strokeWeight(2);
line(0,0,mouse.x,mouse.y);
} |
Weiteres
...
...
- PVector – Referenz auf processing.org
...
- PVector – Tutorial mit Darstellungen
...
- Nature Of Code – Shiffman Seiten 47-83